MADNESS

Introduction

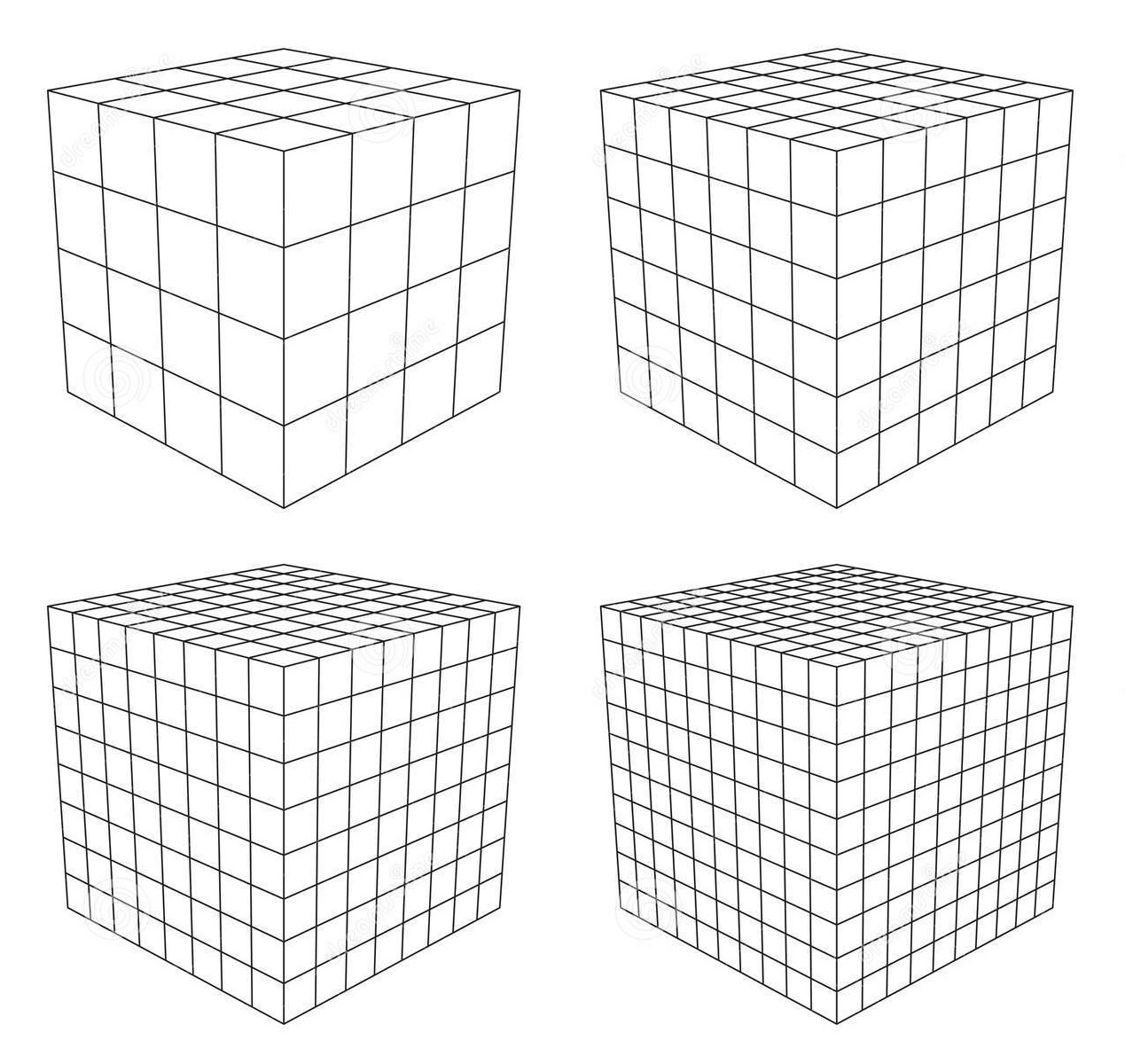
Fig. 1 The number of boxes in a three-dimensional, finite-element grid is vastly different for a slightly different resolutions: see the numbers in table.

Partial differential equations (PDE) are used to approximate solutions to a variety of real world problems. MADNESS (Multiresolution ADaptive Numerical Environment for Scientific Simulation) is a framework written in C++ for solving differential (and integral) equations efficiently on high performance computers (HPC).

A first step to learning MADNESS is understanding the most popular model for solving PDEs: the finite element method scheme which discretizes space (dividing it into boxes) and then creates functions and operators to approximate the solution on the mesh (the discretized space). While this popular approach works for a wide variety of problems, it breaks down for high-dimensional problems that requires resolution at multiple length-scales.

Memory usage as a function of \(N_{size}\).
\[N_{side}\]	\[N_{total}\]
4	64
6	216
8	512
10	1000

As a practical example, suppose you are interested in modeling three dimensional (3D) water waves on a finite element grid. DEFINE BOX as ELEMENT Now suppose you need to include the interaction of the large ocean waves with the small waves of an outboard motor; this is a problem with multiple length scales. Large waves require a large total simulation volume, while small waves require a tiny volume units. This combination uses lots of memory, and will scale poorly when increasing the resolution. The memory footprint is proportional to the total number of boxes or elements \(N_{total}\), for

\[\text{Memory size} = O(N_{side}^3). \]

A high-dimensional, high-resolution problem is the weakness of the finite element method. When possible, it is advantagous to use the fewest number of dimensions that adequately capture the phenomenon. For instance, given a spherically symmetric electron cloud in the presence of a linearly-polarized electric field, cylindrical symmetry is imposed on the system. This makes a 2D simulation is sufficient; an elliptically-polarized laser, however, breaks the cylindrical symmetry requiring a 3D simulation.

1D and most 2D problems can be solved on personal computers; however, when increasing complexity outpaces the abilities of a personal computer, small workstations (or cloud computing) are the next solution. These use multiple of processors (with dozens of computing cores) and can be built with over 100 GB of shared memory. In shared memory computers, memory size (or processing power) is the bottleneck. However, some simulations (supernova, weather, molecular dynamics, etc.) require the largest computers, and these use distributed memory. In these systems, interprocessor communication becomes the bottleneck. While supercomputers will always be improving bus speeds, fiber optic interconnects, network topology, and routing algorithms; users must create code to take advantage of these technologies.

MADness: a Multiresolution ADaptive mesh

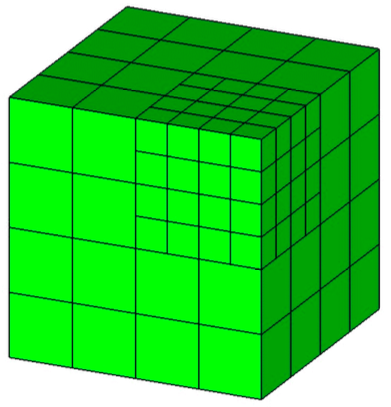
Fig. 2 A multiresolution mesh has more than one size box in the grid, and an adaptive grid places extra grid points just where they are needed.

One way of solving the issue of multiple length-scales on a high-dimensional domain is to introduce a multiresolution (variable-size) mesh shown in Fig. 2. Multiresolution is the M in the MADNESS acronym.

Multiresolution grid placement is challenge: will small ripples stay in one place or will they move over time? To solve this issue, MADNESS uses an ADaptive (mADness) mesh: one that changes to meet the needs of the function being modeled. If you're interested in the mathematical details of adaptive refinement, see section 2.1 of our SIAM Publication.

madNESS: a Numerical Environment for Scientific Simulation

This numerical environment for scientific simulation (madNESS) consists of the following features:

A library of fast, arbitrarily-accurate math functions acting on simulation-domain functions.
The illusion of "basis-free" computing.
A parallel runtime environment engineered for load balancing on hundreds of thousands of cores.
An overview of the HPC libraries upon which MADNESS is based.

In the early days, much was learned about engineering HPC applications by trial and error. For instance, when writing a 3D finite element algorithm on a 64 CPU-cluster, one might naively allocate 1 CPU for each element of a 4x4x4 grid (see Fig. 1). This poor design-choice locks the hardware to the simulation-parameters, limiting code portability and a future growth in computing power: Moore's Law.

Many HPC applications are writen by scientists working outside their domain of expertice. Over the years HPC frameworks have evolved to ease the transition, and MADNESS has had the benefit of standing on the shoulders of giants. One such luxury is having computational objects that directly correspond to terms in the equation we are modeling. Other HPC frameworks, by contrast, force programers to work with computational objects that are non-physical abstractions (e.g. processorID). These hurdles make HPC development needlessly complex.

HPC API

A 3D finite-element scheme stores the data of the simulation function (ocean waves, or electron wave function) in a fixed, 3D array. MADNESS functions, due to their adaptive nature are stored as a tree. To facilitate fast, guaranteed precision math on this tree, MADNESS provides an application programming interface (API) for common operations for functions of one to six dimensions. These operations include: arithmetic, linear algebra, numerical differentiation, and integral convolution. This API enables the creation of code that often reads like the math equation that it is modeling. For an example see section 3 of the SIAM publication.

"Basis-free" computing

Many simple chemical systems are efficiently modeled using a molecular-orbit basis. These basis functions reflect the symmetry of the system, and chemical processes near the ground state are accurately described with just a few molecular-orbital basis functions. This is referred to as a sparse basis, and is computationally beneficiais computationally beneficial

While a sparse basis makes for efficient computation, it has a dark side: basis error. For low-energy processes (between the ground state and first excited state), the basis error is small. However, as higher-energy chemical processes involve more exotic excitations more basis functions are requred which amplifies basis error. For these systems, MADNESS (like a finite element scheme) becomes an attractive solution that doesn't have basis error. However, being more memory-efficient, MADNESS outperforms the finite elements scheme which is seen as a dense solution to the problem.

Load-balancing

There are physical limits on processor speed; for this reason, HPC is synonymous with distributed computing. Today, the most powerful computers have the most processors. Computers with thousands of available processors are no longer rare at universities and government labs. However, writing efficient code to make use of these computers is a challenge.

An important test for HPC software is the scaling test: benchmarking code speed as a function of the number of processors on which it is run. Creating code whose speed scales linearly with the number of processors is the main goal in HPC. IMPROVE SENTENCE Scaling measures the efficiency of processor use. While more processors usually brings more speed, in reality the law of diminishing returns eventually takes over.

MADNESS successfully scales to thousands of processors; this is due in part to its internal compartmentalization of work for its task-queue that is designed to hide interprocessor communication latency. To learn more about the task queue read section 4 of the SIAM publication.

HPC Libraries

Creating code that can take advantage of modern supercomputers can be a career. Unfortunately, most scientists already have a career, and can't afford to put it on hold while mastering distributed computing software development. The following technologies allow average programmers (through MADNESS) to leverage industry standard:

Global Arrays an API for shared memory programming on distributed memory computers.
MPI Message Passing Interface for distributed-memory parallel programming.
OpenMP an interface to shared-memory parallel programming.
Pthreads a thread execution model governing non-concurrent bundles of computation.
Futures a C++ standard providing synchronization across threads.

Publications

The SIAM publication is a scholarly introduction to the mathematics of MADNESS that describes the distributed computing technologies it relies on and reviews some scientific applications.

My Physics Review A publication solves the time-dependent Schrodinger equation in a strong laser field using MADNESS. It provides an introduction to MADNESS to the atomic physics community.

Here is a brief, 15-minute overview of MADNESS from its founder Robert Harrison.