Concave slope
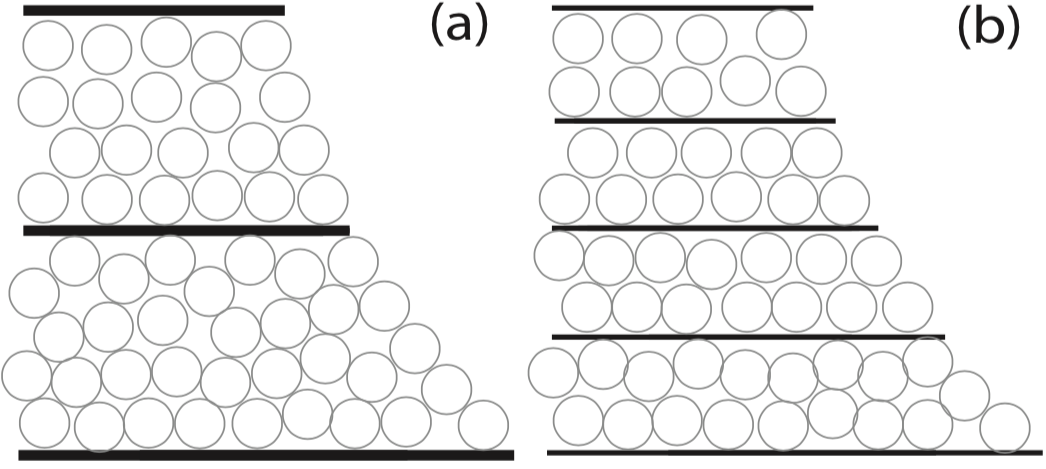
Fig. 1 The representation of a discrete slope as modeled by metal sheets resting on ping pong balls.
Landscape developers (civil engineers) often need a hill decline in elevation as rapidly as possible. While the construction of a retaining wall is an expensive last resort, most prefer an inexpensive, aesthetically-pleasing hillside.
Before Global Positioning Systems (GPS) spawned precision-tractors, engineers created constant-slope hillsides. Unfotunately, this linear slope is not
optimized for a rapid elevation decline
optimized for erosion, and
aesthetically pleasing.
Now that GPS-tractors can make concave slopes, the world will benefit from optimizing their shape.
In the 1960s, Sokolovskii described the optimal form of these slopes as the solution to boundary value problems. However, Isaac Jeldes approximated Sokolovski's boundary value problem with a simple integral. He tested his approximation's integrity with a finite element analysis scheme, and asked me to help him justify the approximation theoretically. We approximated the tangent with the first term of its Taylor expansion \[tan(x) \approx x.\] This is justified for small angles and transforms the differential equation into one with an integral solution. This is a big win, because only a small subset of graduate-level engineers solve non-trivial differential equations; while calculus is a more commonly-used tool in the engineers toolbox.